Dùng hình học hữu hạn, các nhà toán học hé lộ số vé tối thiểu người chơi cần mua để trúng xổ số

Bằng cách sử dụng hình học hữu hạn, các nhà toán học tính toán số lượng vé đủ để người chơi giành được một giải thưởng bất kỳ, nhưng không nhất thiết phải là giải độc đắc

Đã từng có người nói đùa rằng, xổ số thực chất là một loại "thuế" nhắm vào những người biết làm toán. Tuy nhiên, có một thực tế không thể phủ nhận rằng, việc phân tích toán học thực sự có thể giúp người chơi xổ sổ hiểu được xác suất phức tạp liên quan tới một trò chơi luôn được coi là may rủi này.

Chẳng hạn, liệu chúng ta có thể sử dụng toán học để tính toán lượng vé số tối thiểu một ai đó có thể mua để đảm bảo chiến thắng hay không? Các nhà toán học tại Đại học Manchester (Anh) đã phát hiện ra rằng câu trả lời là có, nhưng điều đó không có nghĩa là phương pháp này sẽ giúp người chơi xổ số trở nên giàu có.

Đã có nhiều ý kiến về việc liệu các công thức toán học có thể hỗ trợ một phần cho người chơi xổ số nhằm tăng tỷ lệ trúng số hay không. (Ảnh: IFL Science).

Theo trang IFL Science, nhóm nghiên cứu đã xem xét loại hình Xổ số lô tô của chương trình xổ số quốc gia tại Anh, trong đó người chơi chọn sáu số từ 1 đến 59. Mục tiêu của người chơi là đủ may mắn để có cùng những số do công ty xổ số quay được. Một ai đó có thể giành được giải thưởng khi đoán một cặp trúng giải độc đắc (khớp tất cả sáu số), vốn có giá trị là 7,8 triệu bảng Anh (9,9 triệu USD) ở thời điểm hiện tại.

Theo đó, tiến sĩ David Stewart và tiến sĩ David Cushing, 2 thành viên của nhóm nghiên cứu, đã tìm ra cách để khớp được ít nhất hai con số trong tất cả 45.057.474 tổ hợp có thể. Hóa ra, tất cả những gì người chơi cần làm chỉ là mua tối thiểu 27 tờ vé số.

Được biết, để mô tả các tổ hợp có thể xảy ra, nhóm nghiên cứu đã sử dụng một quy trình gọi là hình học hữu hạn, trong đó các tổ hợp số khác nhau được hiển thị dưới dạng các điểm trong hình dạng hình học.

Ở đây, họ sử dụng "mặt phẳng Fano" – một cấu trúc hình học, trong đó các cặp số được vẽ trên hoặc bên trong các hình tam giác và các đường thẳng hoặc đường tròn nối chúng. Mỗi dòng đi qua ba cặp, tạo ra một trong các bộ sáu số có tỷ lệ cao để giành giải độc đắc.

Về mặt toán học, điều hấp dẫn của tính toán trên không phải là để trúng xổ số và kiếm được thật nhiều tiền. Thay vào đó, nhóm nghiên cứu muốn tìm ra số lượng vé tối thiểu mà một người chơi có thể mua để trúng một số loại giải thưởng, ngay cả khi nó không đáng kể chút nào.

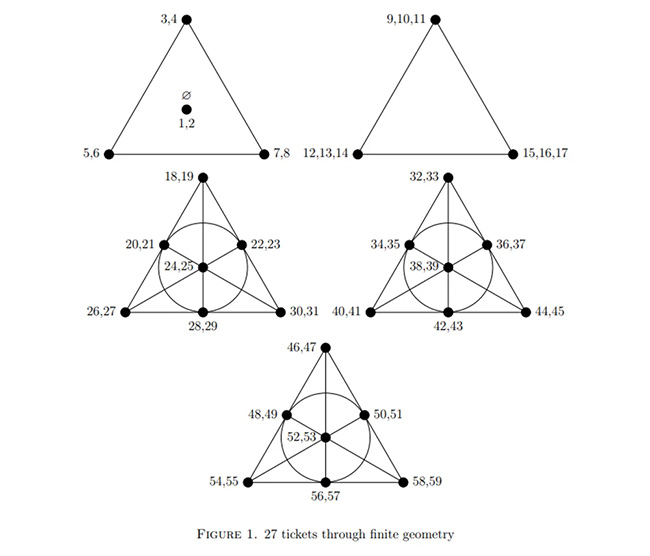
Bằng cách sử dụng hình học hữu hạn, các nhà toán học tính toán 27 vé, với mỗi vé có một bộ số khác nhau, đủ để một người chơi giành được ít nhất một giải thưởng bất kỳ, nhưng không nhất thiết phải là giải độc đắc. (Ảnh: Đại học Manchester).

Toán học giúp trúng số, nhưng chưa chắc đã lãi

Sau khi tính toán, con số 26 vé được toán học coi là rất 'khó nhằn' để một ai đó có thể trúng giải. Trong khi đó, 27 là số lượng vé tối thiểu cần thiết, với mỗi vé phải có một tổ hợp số khác nhau. Đây được coi bí quyết để người chơi ít nhất giành được giải bất kì (không nhất thiết là giải độc đắc).

Tuy nhiên, ở mức giá 2 Bảng Anh cho mỗi vé, tương đương 54 Bảng cho 27 vé, người chơi chưa chắc đã kiếm được lợi nhuận ngay cả khi chiến thắng.

Tại Anh, một người chơi sẽ giành được giải thưởng tiền mặt trị giá 30 Bảng nếu vé có 3 con số trùng khớp với số được quay. Tuy nhiên, người chơi có thể được nhận miễn phí một vé số loại Lucky Dip nếu đoán đúng hai con số. Vé Lucky Dip mang đến cho người chơi một cơ hội 'đổi đời' khác, ngoại trừ việc các con số được chọn ngẫu nhiên cho người chơi.

Theo ước tính của nhà toán học Peter Rowlett, trong 99% trường hợp, khoản đầu tư sẽ không tương xứng với lợi nhuận. Bạn sẽ thắng nhưng không nhiều. Rõ ràng, lý thuyết chỉ có thể hỗ trợ bạn phần nào.

Thực tế, bản thân nhóm nghiên cứu đã thử áp dụng phương pháp của họ vào thực tế. Họ đã mua 27 vé xổ số trước kỳ quay thưởng ngày 1/7 2023. Kết quả, họ có 3 vé trùng ít nhất con 2 số, mang tới 3 vé Lucky Dip miễn phí. Tuy nhiên, cả 3 vé này rút cục đều không trúng giải. Vì vậy, nó giống một phương pháp toán học hấp dẫn hơn là một kế hoạch kiếm tiền nhanh chóng.

Khá thú vị, bản thân phương pháp toán học của nhóm nghiên cứu tại Đại học Manchester cũng thu hút sự chú ý của các các công ty xổ số. Người phát ngôn của Camelot, công ty điều hành Xổ số quốc gia tại Anh, khẳng định nghiên cứu này mang tới nhiều góc nhìn thú vị.

"Cách tiếp cận của chúng tôi luôn là thu hút được nhiều người chơi chi ra càng ít tiền để mua xổ số càng tốt", đại diện của Camelot cho biết.

"Điều quan trọng cần ghi nhớ rằng, cuối cùng, xổ số là xổ số. Giống như tất cả các trò chơi khác dựa trên chương trình xổ số quốc gia, tất cả các số Lotto chiến thắng đều được chọn ngẫu nhiên. Bất kỳ một số nào cũng có cơ hội được rút ra như nhau. Như vậy, mọi dãy số được nhập vào trong một lần rút thăm đều có cơ hội trúng thưởng ngang nhau".

• Đã tìm ra cách dự đoán số trúng thưởng độc đắc?
• Lần đầu tiên phát hiện thứ "tấn công" cả Trái đất, Mặt trăng và sao Hỏa
• Đây là cách người La Mã cổ đại du lịch hơn 2.000 năm trước

Từ khóa liên quan:

vé số

hình học hữu hạn

nhà toán học

công thức toán học

người chơi sổ xố

giải thưởng

trúng sổ xố